In [10]:
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation
plt.style.use('seaborn-darkgrid')
def print_line(line, delimiter):
print('[',end="")
for c in line:
print("{:^3}".format(str(c)), end="")
print(']',end="")
if delimiter:
print(',',end="")
def print_2d_list(input_list):
print('[', end="")
print_line(input_list[0], True)
print()
for row in input_list[1:-1]:
print(" ", end="")
print_line(row, True)
print()
print(" ", end="")
print_line(input_list[-1], False)
print(']')
def is_in_map(grid, x, y):
if x >= 0 and x < len(grid) and y >=0 and y < len(grid[0]):
return True
return False
def valid_step(grid, observed, x, y):
if is_in_map(grid, x, y):
# check if the cell is blocked or has been visited
if grid[x][y] == 0 and observed[x][y] == 0:
return True
return False
def search(grid, heuristic, init, goal, cost, delta, delta_name):
# initial location characteristics
x = init[0]
y = init[1]
f = heuristic[x][y]
g = 0
observed_cells = [[0 for cell in row] for row in grid]
moves = [[0 for cell in row] for row in grid]
expansion = [[0 for cell in row] for row in grid]
# cells that shall be examined next, unless the target has been found
search_queue = [[f,g,x,y]]
found = False
resign = False
while not found and not resign:
# check if there is sill a potential path to the target
if len(search_queue) ==0:
resign = True
else:
# by examining the cell with the smallest f value
# it is guaranteed to find the shortest path if it exists
search_queue.sort()
next = search_queue.pop(0) # cell to be examined
f = next[0]
g = next[1]
x = next[2]
y = next[3]
# check if the cell is the goal
if x == goal[0] and y == goal[1]:
found = True
else:
# expand to new cells if possible
for i in range(len(delta)):
x_next = x + delta[i][0]
y_next = y + delta[i][1]
if valid_step(grid, observed_cells, x_next, y_next):
g_next = g + cost
f_next = g_next + heuristic[x_next][y_next]
# expand the search queue
search_queue.append([f_next, g_next, x_next, y_next])
observed_cells[x_next][y_next] = 1 # so it will not be readded to the search_queue
moves[x_next][y_next] = i
expansion[x][y] = delta_name[i]
return [expansion, moves]
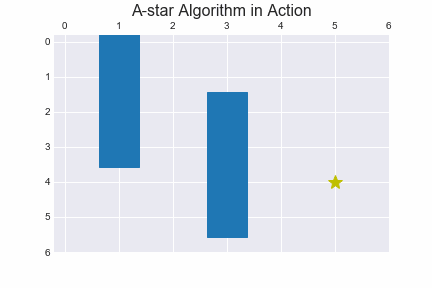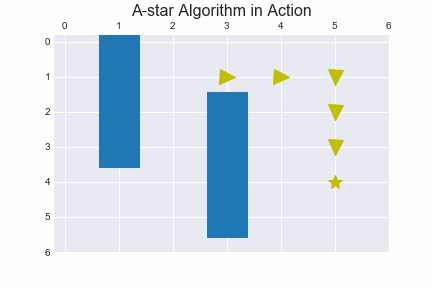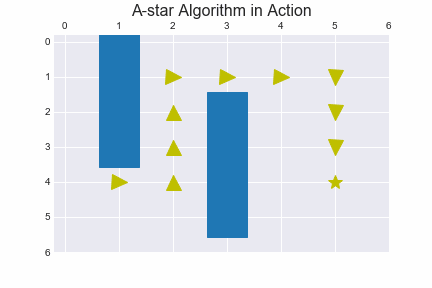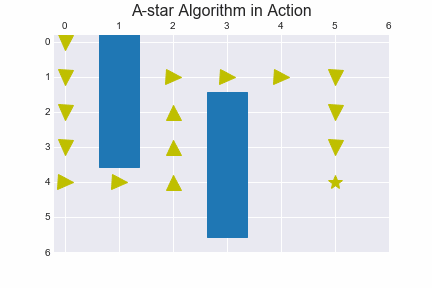
def shortest_path_finder(actions, delta, delta_name, init, goal):
# the shortest path is traced back from the goal location
x = goal[0]
y = goal[1]
policy = [["x" for cell in row] for row in actions]
policy[x][y] = '*'
shortest_path = [[x,y]]
while x != init[0] or y != init[1]: # while we have not reached back to the initial location
x_back = x - delta[actions[x][y]][0]
y_back = y - delta[actions[x][y]][1]
policy[x_back][y_back] = delta_name[actions[x][y]]
x = x_back
y = y_back
shortest_path.append([x,y])
return policy, shortest_path
def main():
grid = [[0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 1, 0, 1, 0, 0],
[0, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0]]
heuristic = [[9, 8, 7, 6, 5, 4],
[8, 7, 6, 5, 4, 3],
[7, 6, 5, 4, 3, 2],
[6, 5, 4, 3, 2, 1],
[5, 4, 3, 2, 1, 0]]
init = [0, 0]
goal = [len(grid)-1, len(grid[0])-1]
cost = 1
delta = [[-1, 0 ], # go up
[ 0, -1], # go left
[ 1, 0 ], # go down
[ 0, 1 ]] # go right
delta_name = ['^', '<', 'v', '>']
expansions, actions_ids = search(grid, heuristic, init, goal, cost, delta, delta_name)
policy, shortest_path = shortest_path_finder(actions_ids, delta, delta_name, init, goal)
print_2d_list( expansions )
print()
print(shortest_path)
print_2d_list( policy )
if __name__=="__main__":
main()
In [ ]: